ループ処理をいくつか使用するので最適なアルゴリズムを考える練習にちょうど良いと思います。
コンパイラの不具合で割り算「/」「%」が使えないことがわかりました。 しかし、*+-など他の演算子は問題なく使用できます。 このコンパイラでも割り算ができるように、 int warizan(int a,int b) のような割り算関数を極力高速になるように注意して作成してください。 速度は、forやwhileのループ回数をカウントすることで代用します。(多重ループの場合はなるべく重複しないようにしてカウントします)
割り算ってなんだったっけ?
10÷2= という計算だと、答えは5です。
10から2が5回引けるから、引ける回数を数えればいいだけですね。
引き算回数式の割り算を作ってみる(回答例1)
引き算回数をする方法で書いてみましょう。
#include <stdio.h>
int warizan(int a,int b)
{
int x = 0, y = 0;
y = a;
if( b == 0 ){
return -1;
}
for(x = 0; y >= b; x++){
y -= b;
}
return x;
}
void main(void)
{
int in1 = 628;
int in2 = 6;
printf("test %d / %d = %d\n", in1, in2, warizan(in1,in2));
printf("sample %d / %d = %d\n", in1, in2, in1/in2);
return;
}
実行結果は上が作った関数の結果、下が普通の割り算の結果です。
$main
test 628 / 6 = 104
sample 628 / 6 = 104確かに答えは正解なのですが、ループ回数が非常に多いですね。
非常にループ回数が多く計算が非常に重いことです。非力な8bitマイコンだと数分掛かる可能性があります。ループ回数が答えですから結果の大きい計算になるほどじかんがかかってしまいます。
ですのでこの答えは60点でできるはできるけど計算が遅いのですぐに改良が求められる答えになります。
筆算のわり算はどんな方法だったっけ?
628÷6の場合はこのように計算して引き算の回数を減らしていませんでしたか?
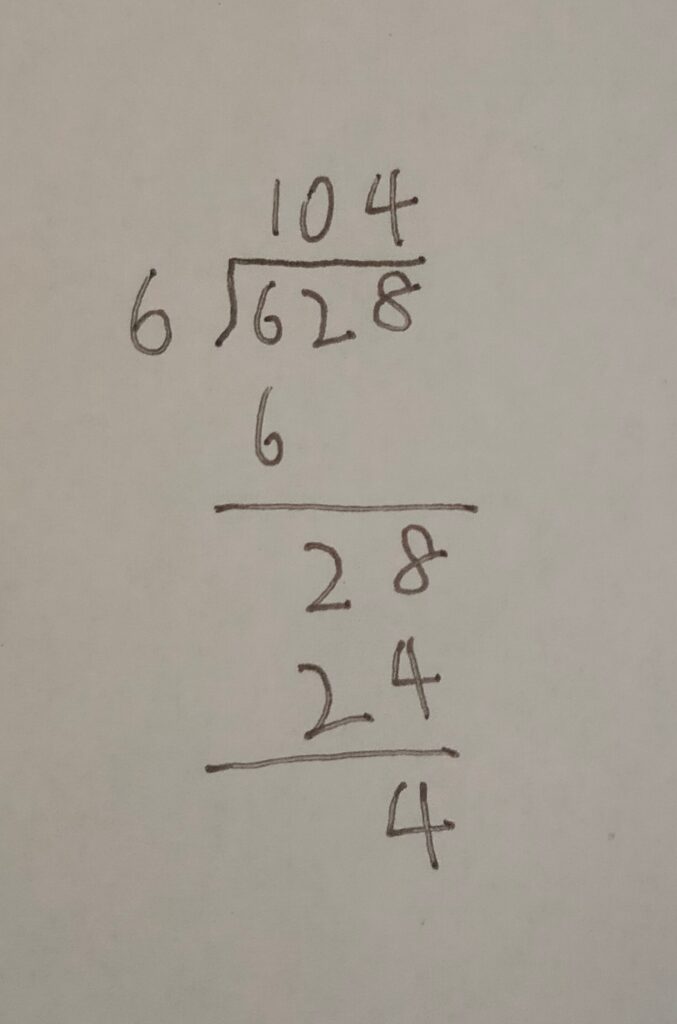
これを素直にプログラムに起こすと(読まなくてもいいです。雰囲気で)
- 6と628を比較 628を超えない
- 6に10かけた60と、628を比較 628を超えない
- 6に100かけた600と、628を比較 628を超えない
- 6に1000かけた6000と、628を比較 628を超えた
- 628から600を引き28と600を比較 600を超えない
- 答えに100を足す
- 6と28を比較 28を超えない
- 6に10かけた60と、28を比較 28を超えた
- 28から6が4回引けることを確認
- 28から24を引き4、答えに4を足す。
- すると答えは104
という流れになります。「手順5」と「手順9」で引き算ループが必要になりますがそれぞれ9回以内なので一旦、許容することにしましょう。
筆算式の割り算を作ってみる(回答例2)
これをプログラミングすると、、、、
#include <stdio.h>
int bekijou(int moto, int jousu)
{
int ret = 1,i;
for(i = 0; i < jousu; i++ ){
ret *= moto;
}
return ret;
}
int warizan(int a, int b)
{
int x = 0, ans = 0, i = 0, j = 1, tmp;
x = a;
if( b == 0 ){
return -1;
}
while(1){
if(x < b * bekijou(10,i)){
if(i <= 0){
break;
}else{
i--;
tmp = bekijou(10,i);
while(1){
if(x < b * j * tmp ){
break;
}
j ++;
}
j--;
ans += j * tmp;
x -= b * j * tmp;
i = 0;
j = 1;
}
}else{
i++;
}
}
return ans;
}
void main(void)
{
int in1 = 6540;
int in2 = 1;
printf("test %d / %d = %d\n", in1, in2, warizan(in1,in2));
if(in2 != 0){
printf("sample %d / %d = %d\n", in1, in2, in1/in2);
}
return;
}
こうなりました。
$main
test 628 / 6 = 104
sample 628 / 6 = 104答えもバッチリです。でも10進数で計算していることで乗数の計算がなんかこう違和感ありませんか?
2進数筆算式の割り算を作ってみる(回答例3)
コンピュータは桁上げるには1bit分、左にずらす(シフト)させるだけなので処理がすごく軽いのです。
16進数だろうが、10進数だろうが、2進数だろうが割り算の方法も結果も変わらないので2進数割り算にしてみます。
#include <stdio.h>
int warizan(int a, int b)
{
int x = 0, ans = 0, i = 0;
x = a;
if( b == 0 ){
return -1;
}
while(1){
if( x < ( b << i ) ){
if(i <= 0){
break;
}else{
i--;
ans += 1 << i;
x -= b << i ;
i = 0;
}
}else{
i++;
}
}
return ans;
}
void main(void)
{
int in1 = 628;
int in2 = 6;
printf("test %d / %d = %d\n", in1, in2, warizan(in1,in2));
if(in2 != 0){
printf("sample %d / %d = %d\n", in1, in2, in1/in2);
}
return;
}
かなりコードが短くスッキリしましたよね。i=0が何度も実行されて無駄なループも多そうな気がします。
最適化した割り算を書いてみる(回答4)
処理のシーケンスを少し工夫してみました。最初からこうしていても良かったですね。
私の最適解というだけで、もっと高速な方法が別にあるかもしれません。
#include <stdio.h>
int warizan(int a, int b)
{
int x = 0, ans = 0, i = 0;
x = a;
if( b == 0 ){
return -1;
}
while(1){
if( x < ( b << i ) ){
break;
}
i++;
}
i--;
while(1){
if(x > b << i){
ans += 1 << i;
x -= b << i ;
}
i --;
if(i < 0){
break;
}
}
return ans;
}
void main(void)
{
int in1 = 628;
int in2 = 6;
printf("test %d / %d = %d\n", in1, in2, warizan(in1,in2));
if(in2 != 0){
printf("sample %d / %d = %d\n", in1, in2, in1/in2);
}
return;
}
まとめ 回数比較
最後に「628÷6」でどれだけ計算回数が減ったかループ回数を数えてみます。
| ループ回数 | |
| 引き算回数式の割り算 | 104 |
| 筆算式の割り算 | 43 |
| 2進数筆算式の割り算 | 21 |
| 最適化した割り算 | 15 |
かなり桁数の少ない計算でも、もともとの14%までループ回数をへらすことが出来ました。もっと良い方法もあるかもしれません。
どの方法でも同じ計算が可能なのですが、アルゴリズムによって5倍以上の速度差が出ました。
このように、アルゴリズムを工夫すると高速な計算が可能だというのが実感していただける演習だったのではないでしょうか。
一度、自分でも書いてみてはいかがでしょうか。

コメント